The Fighting Chess Index

Introduction

The Fighting Chess Index (FCI) is a composite, weighted measure of the combativeness of top chess players. It combines data about the frequency, length and colour of drawn games from 2015-2020 to provide a single score for each individual that can be used to compare the degree of ‘fighting chess’ among players. This article introduces the FCI and the basic methodology, provides current rankings, FAQs, and a technical note with details for replication.

An early caveat: all indices are controversial, to varying degrees. It’s important to note that I have used standard and widely accepted methods to create the index, with as few of my own subjective decisions in the input as possible. I have highlighted where I have made these assumptions and why. I also reran the index under various different assumptions to see if the rankings significantly changed; on the contrary, the FCI is remarkably robust. Players who have very similar scores might swap their rankings depending on the assumptions, but someone ranked 1st will always come out as significantly more fighting than someone ranked 20th no matter which version we use.

Second caveat: I did not create the index to target any particular players, many of whom are my friends and colleagues. Rather, I made it because there seemed to be strong demand among chess fans and even other grandmasters for something like this. I talk a little bit about why some players might have high or low FCI scores, as well as what can and can’t be inferred from the index, but I’m sure further discussion will follow, after which the index can be tweaked and hopefully improved along what most chess fans believe is a truer representation of ‘fighting-ness’.

The FCI is a score out of 100, where a higher score means the player is more ‘fighting’. I used data from the freely available Caissabase (November 2020 version) and included all games from 2015-2020 by players who had played at least 100 games and had an average rating of at least 2400 in this period. Thus, the ‘Top 50’ table below refers to the active players with the highest average rating, according to this database, from their 2015-2020 games.

In general terms, the index is computed as follows. First, I cleaned the database as best I could to merge names for the same player, and remove simul, Chess960 and consultation games, etc. Second, I calculated the percentage of draws, ‘short’ draws and short draws with White, as well as the average length of draws, for each player. I chose 30 moves as the threshold for a short draw as being under 30 moves, in accordance with the Sofia rules. Third, I ran a principal component analysis that, in simplistic terms, combines all of the metrics above, weights them in such a way as to avoid double counting (e.g. it recognises that someone with many short draws will also have a low average draw length), and extracts one number to represent the ‘hidden concept’ that these measures might explain – in this case, “fighting chess”. Finally, I adjusted the scores such that players who more often play players around their own strength, such as in more round-robins, aren’t punished for scoring more draws than similar players who play games with bigger rating differences, such as in large open tournaments.

On to the scores!

FCI: Top 50 Rated Players

Rank FCI Name
1 80.1 Kramnik, V
2 79.3 Le, Q
3 78.9 Navara, D
4 78.4 Caruana, F
5 77.3 Artemiev, V
6 77.0 Eljanov, P
7 76.9 Naiditsch, A
8 76.8 Duda, J
9 76.5 Carlsen, M
10 76.0 Inarkiev, E
11 75.2 Topalov, V
12 73.5 Nakamura, H
13 71.4 Cheparinov, I
14 71.4 Vachier Lagrave, M
15 71.3 Vidit, S
16 71.1 Harikrishna, P
17 71.1 Dominguez Perez, L
18 68.9 Grischuk, A
19 68.9 Andreikin, D
20 68.6 Yu, Yangyi
21 68.5 Nepomniachtchi, I
22 68.5 Matlakov, M
23 68.1 Karjakin, S
24 67.8 Rapport, R
25 67.2 So, W
26 66.6 Ivanchuk, V
27 66.4 Aronian, L
28 66.1 Wei, Y
29 65.9 Wojtaszek, R
30 65.9 Giri, A
31 65.8 Shankland, S
32 64.7 Mamedyarov, S
33 64.1 Gelfand, B
34 64.0 Wang, H
35 63.9 Ponomariov, R
36 63.7 Liren, Ding
37 61.3 Bacrot, E
38 61.2 Bu, X
39 61.1 Leko, P
40 60.9 Malakhov, V
41 60.7 Vitiugov, N
42 59.5 Almasi, Z
43 59.0 Kryvoruchko, Y
44 58.8 Vallejo Pons, F
45 58.7 Svidler, P
46 58.2 Jakovenko, D
47 57.9 Anand, V
48 57.9 Tomashevsky, E
49 57.6 Kasimdzhanov, R
50 51.2 Radjabov, T

 

This is a list of the 50 active players with the highest average ratings in my sample (2015-2020), sorted from most to least fighting. At the top of the list is a surprising name: Vladimir Kramnik, a.k.a. “the man who brought back the Berlin”. But most experts agree that the Kramnik at the end of his career was a different animal to the Kramnik who became World Champion two decades ago. In his final years on the scene, Kramnik seemed to break the shackles and play more for the love of the game, becoming overly (and sometimes even comically) optimistic about his chances in every game. He recorded a short draw in less than 4% of his games in this period, while overall his draws lasted an average of 52 moves.

Ask most GMs and they’ll have no problem agreeing that the other names at the top of the list belong to fighting players. The FCI scores are also pretty tight, and in fact Vlad gets dethroned for top spot by David Navara and Le Quang Liem in some of the index variations I tried. But if you’re like me, you can’t help but cast your eyes down at the bottom of the list. Coming 50th by some distance is Teimour Radjabov. In 2015-2020 he drew more than 60% of his games and played a short draw almost once in every five games. Note that this index doesn’t account for his 2021 games, including the FTX Crypto Cup and the Superbet Classic; nevertheless, the 2022 Candidates contender finishes 50th in almost every variation of the index that I tried.

If you’re like me, the most surprising name to see near the bottom of the list is Vishy Anand, so much so that I went back and manually checked all of his games. Since 2015, Anand played a short draw in roughly one out of every seven games, with an overall draw rate of 55%. On the other hand, some of these short draws may be aimed at conserving energy in blitz and rapid events (i.e., events with multiple rounds per day), and these are more likely to be played with Black (42% of his short draws). But note that the argument about short draws being strategic is not inconsistent with the validity of the FCI. Making short draws to conserve energy and improve one’s tournament position is a potential excuse for a poor score, but that score still represents what most chess fans would agree is a low degree of fighting chess in the games. Still, overall, the Anand in 2015-2020 is a less ferocious tiger than in his days as World Champion, although Kramnik’s score shows that this isn’t always the case. In a future post, I will discuss what happens if we extend the FCI to include games before 2015, as well as compare the scores of the various World Champions throughout history.

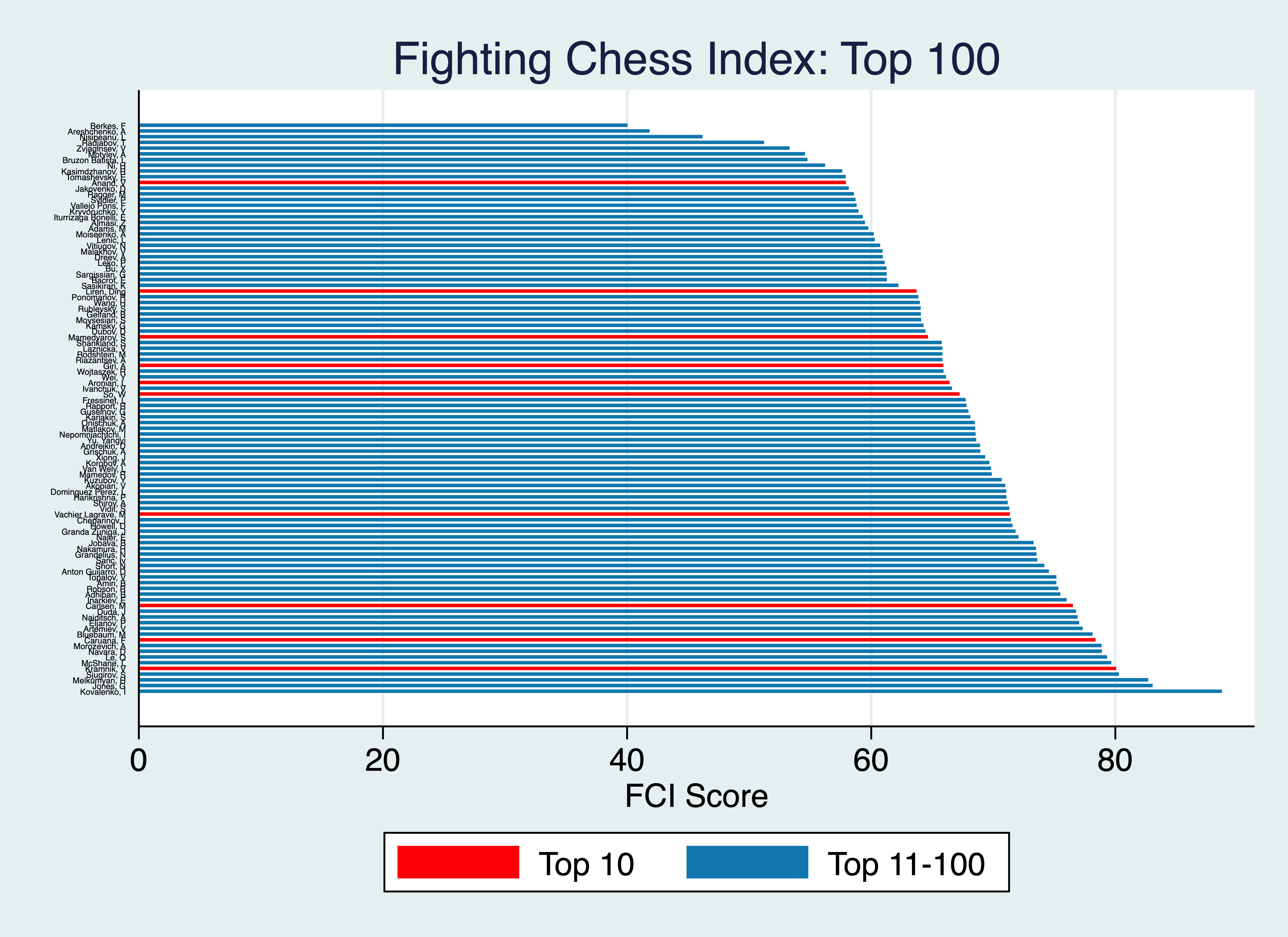
The next graph, which you’ll need a big screen to read, lists the FCI scores for the top 100 players by rating over 2015-2020:

 

 

(You can find the full list in the Appendix at the bottom.)

Highlighted in red are the top 10 players, who, ranked from most to least fighting, are Kramnik, Caruana, Carlsen, Vachier Lagrave, So, Aronian, Liren, Giri, Mamedyarov and Anand. Coming first by some distance is Igor Kovalenko with an FCI score of 88.7. The Ukrainian GM who plays for Latvia drew only 24% of his games in this period, but even more impressively, less than 10% of his draws were short, and almost never with White. Two Englishman – Gawain Jones and Luke McShane – figure among the next 5 most fighting players, along with two Russians (Kramnik and former prodigy Sanan Sjugirov) and the Armenian (and honorary Australian) Hrant Melkumyan.

By the way, the FCI is mainly useful for comparing players. But if you want to try to interpret one individual’s score, note that the average FCI score in the current index is 65.8. Anything above this is above-average for the sample (the often-maligned Anish Giri is above-average by 0.1!), and vice-versa. This is because the FCI scores have been rescaled such that the most fighting player in the whole sample (i.e., active players with an average rating above 2400) has a score of 100 and the least fighting player has a score of 0.

That of course begs the question: who are the two at the ends of the scale?

Coming in with the top score of 100.0 is a Russian IM called Ivan Aldokhin. He is one of a handful of players with a short-draw percentage of less than 1% and who never played a short draw with White in this period (another is the well-known IM Greg Shahade, with an FCI of 94.8). One of the more recognisable names at the top is GM Robert Hess (94.0). When he does draw a game, which happens only 12% of the time, it lasts more than 60 moves on average. Another is GM Valentina Gunina (93.6), who also tops the FCI for female players. Her FCI score is consistent with her recent performance in the FIDE Women’s Grand Prix in Gibraltar, in which she played 10 decisive games in a row before drawing her final round after 135 moves.

You may be wondering where Alireza Firouzja is. Across his 2015-2020 games, Alireza’s average rating was only just too low to appear in the graph of the top 100 rated players. Otherwise, his impressive FCI of 82.4 would place him 4th out of the top 100, or clear 1st out of the top 50.

At the other end, the anchor score of 0.0 goes to GM Igor Stohl. Since 2015, more than half of his games have been short draws, and in fact, about one in four of his games ends in a draw in 15 moves or less. There are some other famous names on this side of the scale that will not surprise many, such as GMs Alexander Khalifman (2.4) and Bogdan Lalic (3.7), who are the only other two players where more than 50% of their games are short draws. But there are also plenty of GMs who make their livings from league matches or as the paid professionals in so-called norm factories, such as the First Saturday tournaments in Budapest, the Third Saturday tournaments in Serbia and the Charlotte Chess Centre’s GM/IM norm events. Milan Drasko (5.3) and Tanguy Ringoir (14.5) are two examples of GMs who regularly take part as the titled cannon-fodder in these events.

I doubt that these players will mind being told that they have a low FCI. The organisers of these events make their money from charging large fees to norm-hunters and only really care that their GMs maintain a sufficiently high Elo so that the norm requirements are not too onerous; there are no incentives for the chess to be entertaining to the public. Likewise, most sponsors of league teams care much more about where the team finishes on the ladder than whether the games are exciting. The incentive structure of these markets doesn’t make for fighting chess – in fact, quite the opposite – and that’s arguably fine seeing as these are typically not spectator events.

Next Steps

I expect there to be feedback and suggestions of varying degrees of usefulness. Few indexes are perfect first time around and it’s quite possible that some of these suggestions will convince me to make alterations to the methodology, which I’ll detail in an update.

I chose to take games since 2015 because I wanted the FCI to be current. But we chess fans are often interested in historical debates, such as “Who was the most fighting World Champion?”. In a future article, I plan to extend this analysis by looking at historical players, gender and country differences, and so forth. In the future, I will probably also try to find some way to extend the index to active players of all ratings and make a searchable database online.

But for now, this article just wanted to introduce the index, and I welcome comments and feedback, which you can leave below or send to me directly. If you’re curious to know your own ranking (and think you played more than 100 games in 2015-2020 with an average rating above 2400), feel free to contact me and I’ll send what I have. The easiest way to get in touch with me is through the contact form on my economics page.

FAQs

Q: “Isn’t it impossible to measure fighting spirit with statistics?”
A: Indexes like the FCI are useful when there is some underlying concept of interest that can’t be directly measured, like a country’s level of corruption or gender inequality. So long as most people agree on the statistics that are likely correlated with the underlying concept – in this case, that measures around the frequency, length and colour of draws are related to fighting spirit – the tool of principal component analysis (PCA) allows us to at least compare two or more players with each other.

Q: “What affects the score?”
A: The variables in the main FCI are: frequency of draws, frequency of draws under 30 moves, frequency of draws under 30 moves with White, and average draw length.

Q: “So, do you just take an average of the four measures?”
A: No. They are weighted automatically via the Eigenvector in the PCA (see the technical note), so that the most important (in terms of ‘explaining variance’) are given a higher weighting.

Q: “But including both short draws and the average draw length is double-counting, right?”
A: Even though they are correlated (someone with lots of short draws is likely to also have a low average draw length), they measure slightly different things, so it’s good to include both. In fact, when running PCA, it’s statistically desirable to include highly correlated variables. The final weightings take care of the main double-counting concern.

Q: “Aren’t stronger players more likely to draw their games because chess is inherently a draw?”
A: Yes. The FCI adjusts for strength, so that, on average, a stronger player with the same stats about their games as a weaker player will have a slightly higher FCI. The adjustment is done statistically.

Q: “Do you take account of whether a player plays in round-robins or Swiss opens?”
A: It’s impractical to classify all of the tournaments in the data, but players whose opponents are normally closer to their own strength, e.g. from round-robins, also get a positive statistical adjustment to their FCI scores.

Q: “How did you choose your sample restrictions?”
A: I chose the last six years and a minimum of 100 games because I wanted a current index of active players. Including players who have played fewer games would risk skewing the index because of a few people with extreme frequencies (e.g. players with 100% short draws). I chose an average rating of 2400+ because I wanted to make sure I included all ‘professional’ players, especially because there are professional 2400-2500 GMs with reputations for making many short draws in norm-factory or league events.

Q: “Why didn’t you just make the index on every player in the database first?”
A: The way that PCA works means that the scores are dependent on the whole sample, so ideally you want to choose the most relevant sample possible. It’s something of a trade-off, but 2400+ playing at least 20 games a year seemed like decent criteria for a reference group for professionals. The rankings change slightly if, for example, we only consider the top 50 players as their own sample (Kramnik drops to third behind Le and Artemiev, though their scores are within 0.6 of each other, and Radjabov is still 50th by roughly 4 points).

Q: “I don’t think that draws by themselves should count. What happens if you ignore them?”
A: Then top players who usually play events with Sofia rules (i.e. no draws before move 30) will typically get a higher score. Even though it is possible to make shorter draws through repetitions, many players who want a draw play conservatively until the peace offering on move 30, which is why there has been a sharp spike in draws at moves 30 and 31 since 2005. Ignoring the overall draw rate in the index sees Carlsen and Topalov move into the top 5 behind Kramnik, Le and Caruana, while Radjabov moves up to 46th and Zoltan Almasi falls to 50th.

Q: “What about including upsets?”
A: To me, upsets are not a good representation of fighting chess, but others may disagree. I included a measure for how often a player lost to (beat) an opponent 150 points lower (higher) rated. The top 5 become: Le, Navara, Kramnik, Caruana and Carlsen, while you can guess who finishes 50th.

Q: “Why didn’t you include any elements of the games themselves, like playing exciting openings or sacrifices?”
A: That’s just too hard to do with the data available. Creating within-game measures is exceedingly computationally intensive, and even if it were done for the current database, I’d have the issue of having to update it all in the future. One way around this is to first compute an excitement score for ECO codes and then include this in the index; I’m working on this for the future.

Q: “Any index that says Anand isn’t a fighting player is broken!”
A: I can appreciate the sentiment, but the Anand of 2015-2020 wasn’t as fighting as some of his peers; the stats speak for themselves.

Q: “What’s the point of this index?”
A: To make some people happy and some people angry. No, seriously, I love chess and data analysis, so to me it’s always interesting to try and combine to two. Lots of people from amateurs to grandmasters have told me that they would be really interested in seeing an index like this, so clearly I’m not the only one.

Q: “My rating’s under 2400/I played less than 100 games. Can you still tell me my ranking?”
A: Write to me through the contact form, and I’ll see what I can do.

Q: “What’s your FCI? I bet you made it super high.”
A: I have been basically retired since 2017 so I didn’t make the cut, having only played 65 games during the period. But I manually computed my FCI anyway: 63.5, slightly less fighting than the average.

Technical Note

Here, I provide a bit more detail about the method used to compute the FCI. I wrote my code in Stata and am happy to share my .do file on request. Given that the data is publicly available, the details below should already be enough for replication in most statistical languages; in particular, there are several online resources for how to replicate Stata commands in R or python.

I chose the Caissa database because it’s publicly and freely available, which makes it easier for others to replicate or improve on my analysis. The downside is that the database isn’t as well cleaned as paid versions (e.g. my old World Cup nemesis, Leinier Dominguez, appears in half a dozen forms, and most Chinese names appear in two forms with the first and last names swapped). I used the 2020-11-14 version and opened the .si4 file in ScidvsPC (actually I used the Mac equivalent), which is also freeware. Scid has an option to export a gamelist directly to a text file, which avoids messy PGN parsing.

After importing the text file, I dropped games played before 2015. Before manual cleaning I used string matches on the event and name variables to drop Chess960, simul and consultation games and games by engines, followed by some manual cleaning. I turned each game observation into two observations, one for each observed player. I used the function extrname from the Stata dm13 package to make a first pass at merging variations of the same player’s name, and then manually checked and cleaned the names of all players with ratings above 2500. I did not manually check players below this, so if a player with a rating of 2400-2500 had two or more name variations with a minimum of 100 active games since 2015 in each variation, that player would have multiple entries in the final dataset. The chances of this are very low, and in the future, I will attempt manual cleaning of this rating range, but because the rankings of interest concern much stronger players, this is unlikely to affect the index.

Then I generated the following variables for each player and collapsed the dataset to the player level, keeping those with eloav > 2400:

• N: total games
• eloav: average rating across N
• elodiff: average absolute difference in ratings across N
• d: number of draws / N
• d_short: number of draws in 30 moves or less / N
• d_short_W: number of draws in 30 moves or less where player was White / N
• d_length: average number of moves for drawn games

The final dataset contained 1,458 players. It is relative to this ‘peer group’ that a player’s fighting chess is assessed. I merged this dataset on names with the current FIDE ratings data in order to get gender, age, country and title data. (I did not use the merged data to generate the index, but it was useful for seeing which top players were left out due to low activity, as well as to run subsequent subsample analysis by gender etc.) I then generated the first iteration of the scores using Stata’s inbuilt PCA function on the variable list {d, d_short, d_short_W, d_length}. The first component had an Eigenvalue of 3.415, substantially larger than the second-largest component (0.406), so we can confidently retain only the first component. Its corresponding Eigenvector was {0.454, 0.532, 0.519, 0.492}.

Because the probability of a draw increases with the strength of players (chess is, after all, a draw) and with the closeness of the two players’ ratings, I then ran a linear regression of the first component of the PCA on eloav and elodiff and used the predicted residuals. In theory, this should to some extent control for any bias coming from stronger players who play round-robins being unfairly disadvantaged by the index, although other options (such as allowing for non-linearities) are of course also possible. I then reversed the index and rescaled it on [0,100] via replace FCI = (`r(max)’ – FCI) / (`r(max)’ – `r(min)’) * 100, where r(max) and r(min) refer to the sample maximum and minimum FCI values before the transformation.

For robustness, I ran a number of other variations of the index, such as including different combinations of variables in the PCA, including an “upset” measure (frequency of games with a >150 rating point upset), different sample rating thresholds, different sample time periods, and different definitions of the maximum number of moves for a short draw. Overall, the indexes were very similar in their rankings of the top 50 players (by eloav), with correlations exceeding 0.85.

Appendix: Top 100 Rated Players

Rank FCI Name
1 88.7 Kovalenko, I
2 83.1 Jones, G
3 82.7 Melkumyan, H
4 80.3 Sjugirov, S
5 80.1 Kramnik, V
6 79.7 McShane, L
7 79.3 Le, Q
8 78.9 Navara, D
9 78.9 Morozevich, A
10 78.4 Caruana, F
11 78.1 Bluebaum, M
12 77.3 Artemiev, V
13 77.0 Eljanov, P
14 76.9 Naiditsch, A
15 76.8 Duda, J
16 76.5 Carlsen, M
17 76.0 Inarkiev, E
18 75.5 Adhiban, B
19 75.3 Robson, R
20 75.2 Amin, B
21 75.2 Topalov, V
22 74.6 Anton Guijarro, D
23 74.2 Short, N
24 73.6 Saric, Iv
25 73.5 Grandelius, N
26 73.5 Nakamura, H
27 73.3 Jobava, B
28 72.1 Najer, E
29 71.8 Granda Zuniga, J
30 71.6 Howell, D
31 71.4 Cheparinov, I
32 71.4 Vachier Lagrave, M
33 71.3 Vidit, S
34 71.2 Shirov, A
35 71.1 Harikrishna, P
36 71.1 Dominguez Perez, L
37 71.0 Akopian, V
38 70.7 Kuzubov, Y
39 69.9 Mamedov, R
40 69.8 Van Wely, L
41 69.7 Korobov, A
42 69.3 Xiong, J
43 68.9 Grischuk, A
44 68.9 Andreikin, D
45 68.6 Yu, Yangyi
46 68.5 Nepomniachtchi, I
47 68.5 Matlakov, M
48 68.5 Onischuk, A
49 68.1 Karjakin, S
50 68.0 Guseinov, G
51 67.8 Rapport, R
52 67.7 Fressinet, L
53 67.2 So, W
54 66.6 Ivanchuk, V
55 66.4 Aronian, L
56 66.1 Wei, Y
57 65.9 Wojtaszek, R
58 65.9 Giri, A
59 65.8 Riazantsev, A
60 65.8 Rodshtein, M
61 65.8 Laznicka, V
62 65.8 Shankland, S
63 64.7 Mamedyarov, S
64 64.4 Dubov, D
65 64.3 Kamsky, G
66 64.1 Movsesian, S
67 64.1 Gelfand, B
68 64.0 Rublevsky, S
69 64.0 Wang, H
70 63.9 Ponomariov, R
71 63.7 Liren, Ding
72 62.2 Sasikiran, K
73 61.3 Bacrot, E
74 61.3 Sargissian, G
75 61.2 Bu, X
76 61.1 Leko, P
77 60.9 Dreev, A
78 60.9 Malakhov, V
79 60.7 Vitiugov, N
80 60.3 Lenic, L
81 60.2 Moiseenko, A
82 59.8 Adams, M
83 59.5 Almasi, Z
84 59.3 Iturrizaga Bonelli, E
85 59.0 Kryvoruchko, Y
86 58.8 Vallejo Pons, F
87 58.7 Svidler, P
88 58.6 Ragger, M
89 58.2 Jakovenko, D
90 57.9 Anand, V
91 57.9 Tomashevsky, E
92 57.6 Kasimdzhanov, R
93 56.2 Ni, H
94 54.8 Bruzon Batista, L
95 54.6 Motylev, A
96 53.3 Zvjaginsev, V
97 51.2 Radjabov, T
98 46.2 Nisipeanu, L
99 41.8 Areshchenko, A
100 40.0 Berkes, F

Edits:

• Regenerated table and graph due to duplicate Ding Liren and Yu Yangyi (h/t @AlfJerez). Quoted FCIs change by 0.0 on average and at most 0.1.